State Space Framework: Flexibility to dogmatic rules in biology

Reconciling incongruent rules of deterministic decision making.

In biology (and many other disciplines), linear logic pathways of causation (A->B->C) are often used to describe molecular pathways, cell fates, etc. However, these linear pathways are acutally embedded in complex networks.

With the influx of “omic” data, the conceptually simple idea of nested binary choices is beginning to be undermined. This comes with the realization of vastly more complicated molecular networks with many circular control loops which can be rarely explained through linear causal explanations.

“Omic” data is data gathered from studies that investigate biological molecules. For example, genomic data is data related to the genes, transcriptomics is data related to RNA transcripts, metabolomics is data related to metabolites, phenomics is data related to phenotype, etc. There are multiple different kinds of “omic” data, but ultimately they function to give a more precise characterization of the phenomena at the scale of the “omic” data.

Circular loops

The fundamental issue with networks of regulatory pathways is they fail to distinguish between network architecture and network dynamics. Network architecture is defined as a static collection of nodes (representing genes, proteins, etc) and arrows (representing interactions).

The architecture of genome-wide regulatory networks that encompass all genes is hardwired in the genomic sequence through interacting domains and regulatory proteins/elements.

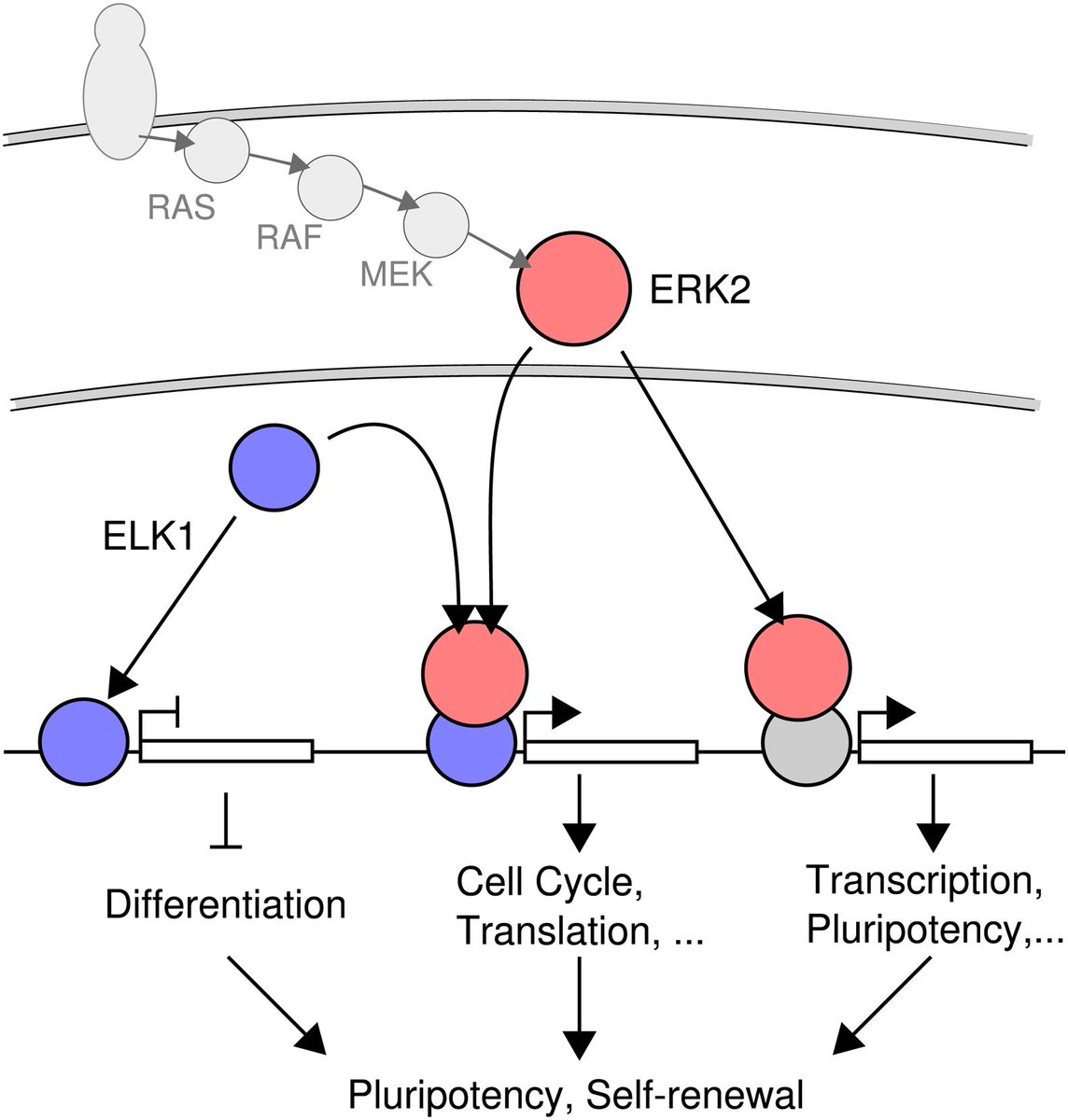
Regulatory Network

source: unknown at this moment

However, network dynamics is the concept that links network architecture and cell behaviour.

The idea of a state space framework aims to combine the far too simple and limiting pathway-based causality scheme with the dynamics of cellular activity to explain phenotype/behaviour. Arrows connecting genes still serve as symbols of causation, however, such linear interpretations of causal network connections fail to consider the context of the entire networks in which all these causal interactions are embedded.

One could theoretically follow the logic for the expression levels of gene X, however with thousands of genes involved that change their expression regarding a certain phenotype, it is very easy to quickly lose track.

Thinking hard

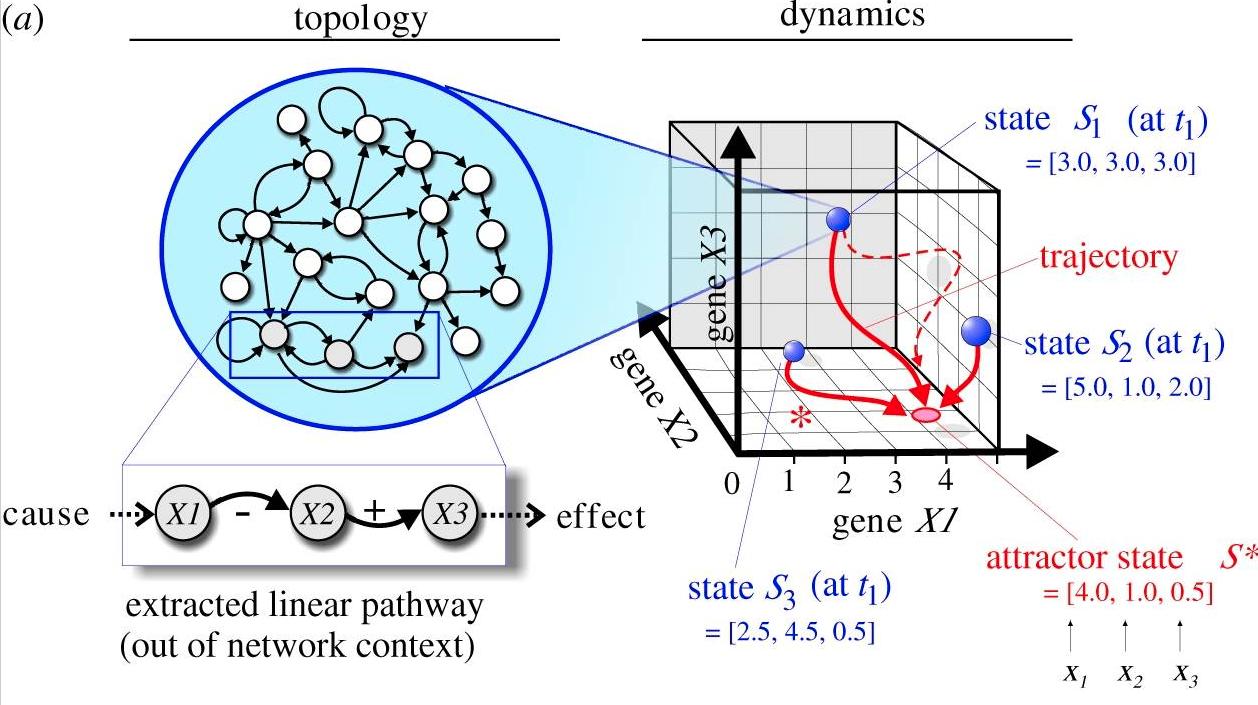
The state space framework is a tool that allows us to understand these dynamics while preserving network architecture complexity. To visualize, a network state S(t) at time t, is defined by the expression levels of all the genes in the network at that specific time (t).

Think of it like a cartesian graph (akin to dimensionality reduction to find an underlying manifold), where each gene is a dimension. As we measure more variables, we increase the number of axes/dimensions (N). The state S(t) is a single point in the continuous, N-dimensional space, the state space, which contains ALL POSSIBLE states.

A manifold is a lower-dimensional subspace underlying population activity that is generally embedded in a higher-dimensional state space. Generally, you do not need to preserve the original N-dimensional state space. Rather, you can reduce dimensions to capture uncorrelated (high variance explaining) information. A manifold can also be modelled on a euclidean space.

Cartesian

source: unknown at this moment

If we have three genes (N=3), the expression pattern of these genes at a particular cell state at time (t) for a behaviour, phenotype, etc is described described by the 3-variable coordinate position at that specific time (e.g., S(5 mins) = [4,3,2.5])

The dynamics come in when we execute all the regulatory interactions between the genes, defined by the network architecture (i.e., let the cell do it’s natural thing), and observe how the N-dimensional gene expression profile changes in a coordinated manner across time.

Each state is represented by a position. As you continue to measure the same variables across time, the position changes. The state moves along a trajectoy in the state space as the genes exert their regulatory actions onto each other according to the network architecture. Thus, the genome, via the regulatory network it encodes, constrains the movement of the state of each cell.

The network architecture is a static entity, because the genome does not change much in a lifetime, that constrains the alterations in the expression values of the genes. Development, homeostasis, behaviour, etc. takes place within these constraints.

The idea gets interesting when you find states where trajectories in the state space environment seem to converge - called attractor states. Attractor states represent stable cell states like differentiated cell types. These attractor states are characterized by a stable gene-expression profile that are often robust to small perturbations since they would attract all unstable points in their neighbourhood (because of regulatory interactions).

Drugs, environment, etc. can cause a state to deviate transiently but if not too large, will return to the attractor state and re-establish the associated specific gene-expression profile.

Since various sets of initial states can end up in the same attractor state, there are many ways to reach an attractor (which is a hallmark of stability).

In real systems with noise, chaos contributing to random fluctuations, the state point (S) wiggles locally in the state space.

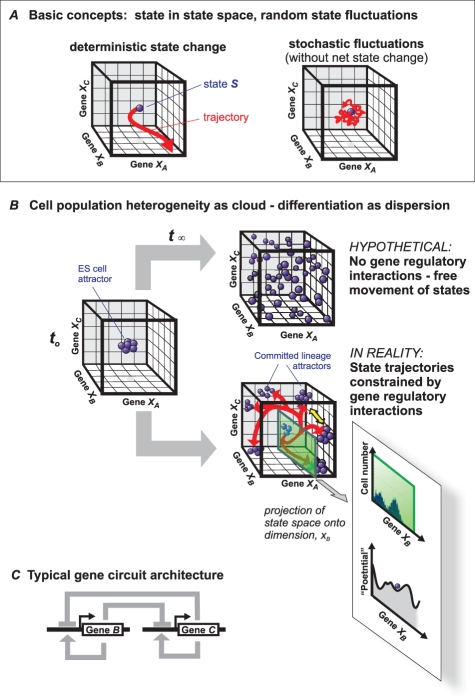
Coordinated change

source: 10.1371/journal.pbio.1000380

A big proponent of the state space framework/fitness landscape/combinatory phase space perspective is Stuart Kauffman. He showed that with a broad class of complex networks with random architecture (wiring), you can produce “interesting cell behaviours”. Then with evolution, you’d need only to fine-tune the state space to optimize the developmental trajectories to ensure smooth descent into attractors of mature cell types and prevent getting stuck in unused attractors of immature regions of the state space (e.g., cancer).

The best part of this framework is that it can be used to describe any dynamical system (e.g., cognitive/motor processes, cell behaviours, telecommunications, weather, etc). Although the big limitations are acquiring enough of the continuous data and computational cost.

In science it is sometimes rare to find people competent in both the math/CS side of analysis while being able to understand the biology to make appropriate interpretations. This highlights the neccessity for cross-functional collaboration. With scientific big data and multi-omic big data on the rise, I hope to see this approach used more.